Equation x g(x) = 0 is a xed point of the function g(x), meaning that is a number for which g( ) = The Newton method x n1 = x n f(x n) f0(x n) is also an example of xed point iteration, for the equation x = x f(x) f0(x) EXISTENCE THEOREM We begin by asking whether the equation x = g(xLearn how to solve f(g(x)) by replacing the x found in the outside function f(x) by g(x)Where F and G are two arbitrary C2function Then, since u(x,y) = w(ξ(x,t),η(x,t)), we find that u(x,y) = F(xct) G(x−ct) (62) Conversely, if F and Gare of class C2, then udefined by u(x,t) = F(x ct) G(x−ct) is a classical solution of (61) T The families of lines x−ct= constant and x
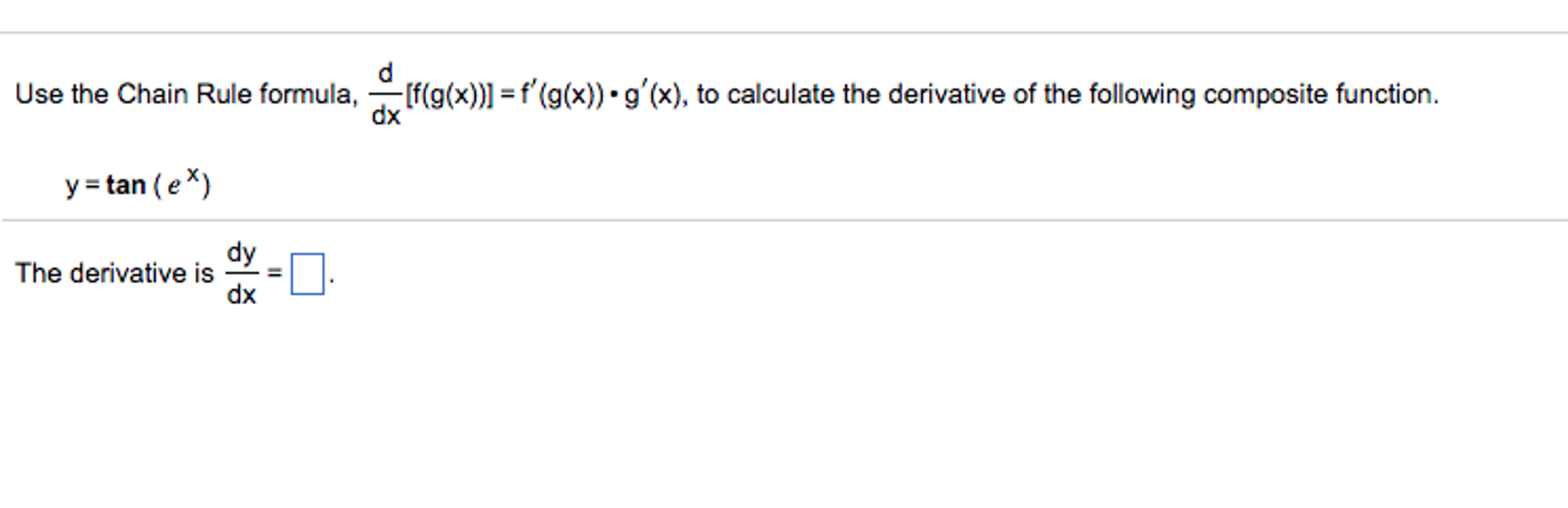
Solved Use The Chain Rule Formula D Dx F G X F G X Chegg Com
F(x)^g(x) derivative formula
F(x)^g(x) derivative formula-F(x)=2x/(x3) and g(x)=x2 find a formula, in simplest form, for (f०g)(x) f०g(x) means to substitute the right side of g(x) for x in the right side of f(x) f(x) = , g(x) = x2 Substitute the right side of g(x), which is (x2), for x in the right side of f(x)Mar 03, 18 · Explanation Given ⎧⎪ ⎨⎪⎩f (x) = x2 1 g(x) = 2x h(x) = x − 1 One way of thinking about these function compositions is to go back and forth between the symbols and verbal descriptions of what the functions do In our example f takes the square of a number and adds 1 g doubles a number h subtracts 1 from a number




Composite Functions Video Lessons Examples And Solutions
Alternatively, by letting h = f ∘ g (equiv, h(x) = f(g(x)) for all x), one can also write the chain rule in Lagrange's notation, as follows h ′ ( x ) = f ′ ( g ( x ) ) g ′ ( x ) {\displaystyle h'(x)=f'(g(x))g'(x)}Letting u = g(x)and v = f (x)and observing that du = g (x)dxand dv = f (x)dx, we obtain a Quotient Rule Integration by Parts formula dv u = v u v u2 du (2) As an application of the Quotient Rule Integration by Parts formula, consider theFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor
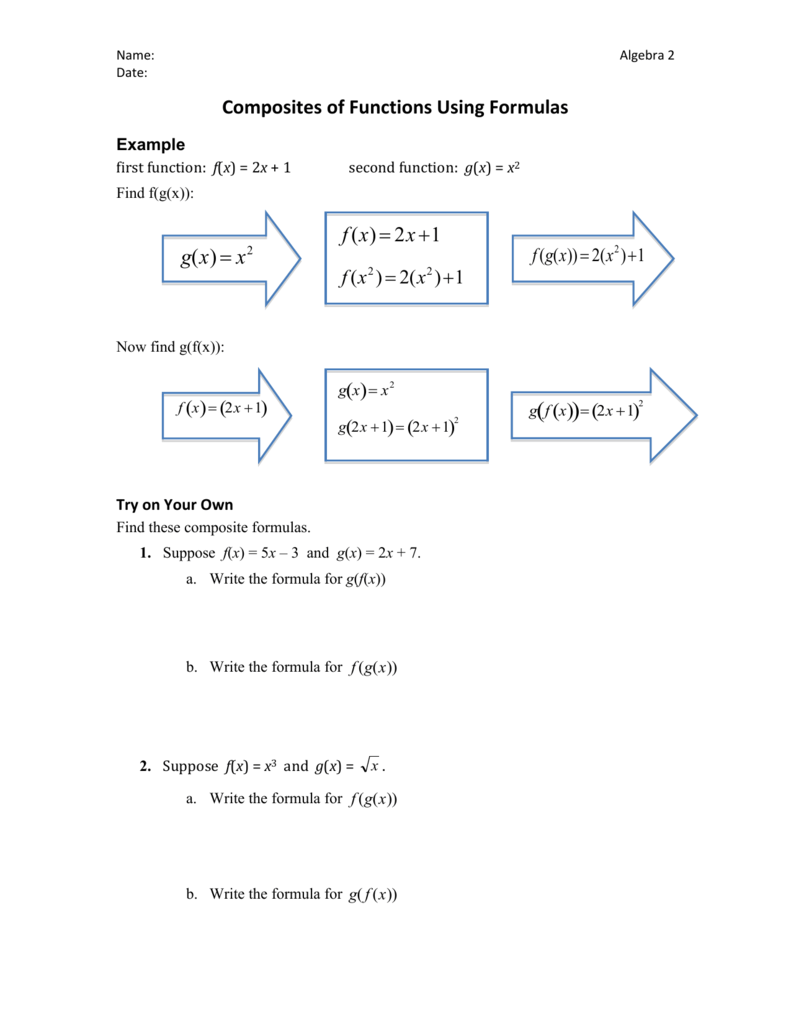
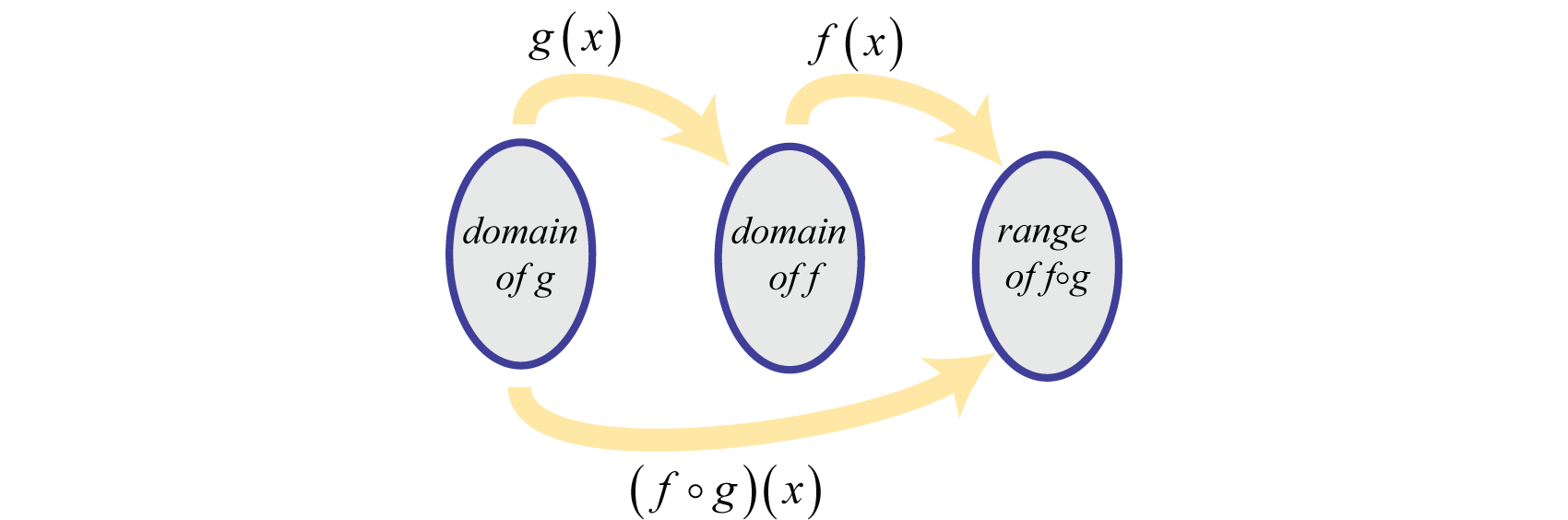
(fg)(x) o = f(g(x)), the g function is inside of the f function (gf)(x) o = g(f(x)), the f function is inside of the g function (fg)(x) o and (gf)(x) o are often different because in the composite (fg)(x),o f(x) is the outside function and g(x) is the inside function`f(x)=4x3` `g(x)=(x3)/4` `f(x)=x/(x1)` `g(x)=(2x)/(2x1)` Domain, Range, Inverse, Vertex, Symmetry, Directrix, Intercept, Parity, Asymptotes of a function calculatorWwwmathportalorg Integration Formulas 1 Common Integrals Indefinite Integral Method of substitution ∫ ∫f g x g x dx f u du( ( )) ( ) ( )′ = Integration by parts ∫ ∫f x g x dx f x g x g x f x dx( ) ( ) ( ) ( ) ( ) ( )′ ′= − Integrals of Rational and Irrational Functions
Completing the square, f(x)=\frac{3}{4}(\frac{1}{x}\frac{1}{2})^2, so x=2 is a global minimum, and there is no minimum, absolute or relative, for x\gt 1 Completing the square, f ( x ) = 4 3 ( x 1 2 1 ) 2 , so x = − 2 is a global minimum, and there is no minimum, absolute or relative, for x > − 1In all the formulas below, f' means \( \frac{d(f(x))}{dx} = f'(x)\) and g' means \(\frac{d(g(x))}{dx}\) = \(g'(x)\) Both f and g are the functions of x and differentiated with respect to x We can also represent dy/dx = D x y Some of the general differentiation formulas are;Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor




Using The Langrange Inversion Formula Mathematics Stack Exchange
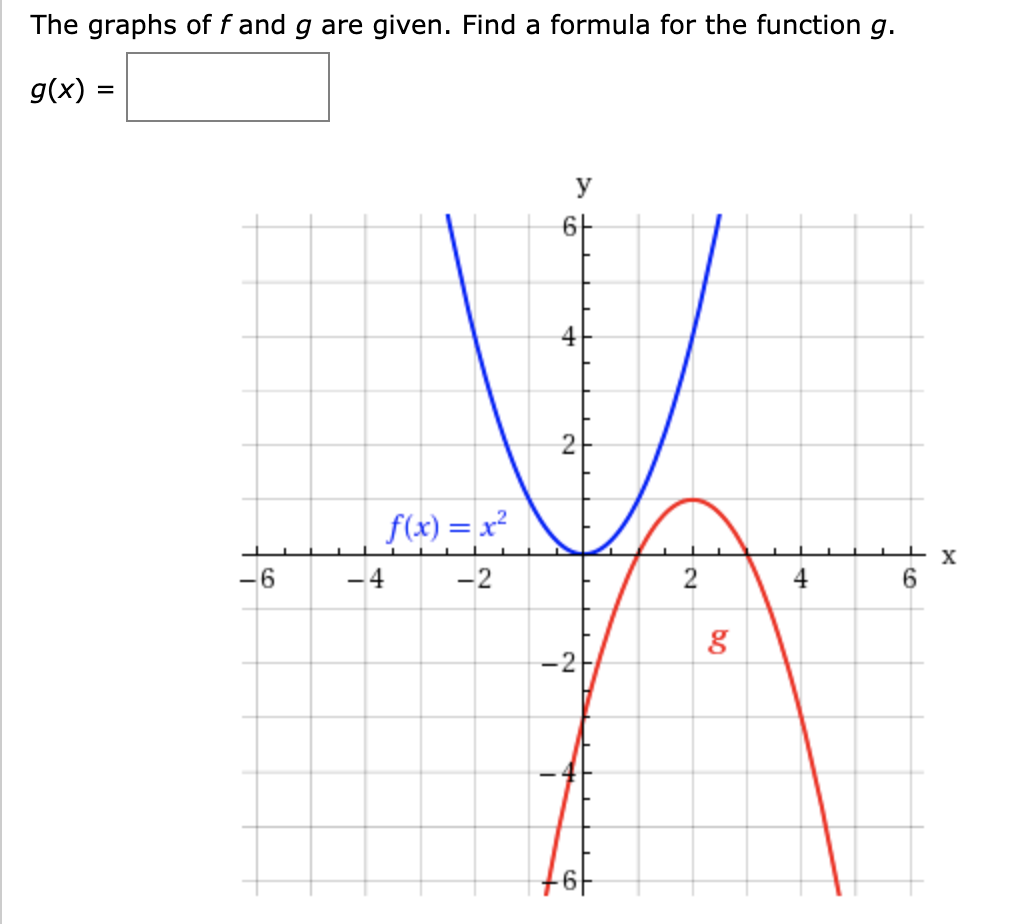



Answered The Graphs Of F And G Are Given Find A Bartleby
The integrand is the product of two function x and sin (x) and we try to use integration by parts in rule 6 as follows Let f(x) = x , g'(x) = sin(x) and therefore g(x) = cos(x) Hence ∫ x sin (x) dx = ∫ f(x) g'(x) dx = ( f(x) g(x) ∫ f'(x) g(x) dx) Substitute f(x), f'(x), g(x) and g'(x) by x , 1, sin(x) and cos(x) respectivelyThe equation is in standard form gx=12 g x = − 1 2 Divide both sides by g Divide both sides by g \frac {gx} {g}=\frac {12} {g} g g x = g − 1 2 Dividing by g undoes the multiplication by g Dividing by g undoes the multiplication by gFind (fg)(x), (fg)(x), (f*g)(x) and (f/g)(x) for each f(x) and g(x) 2 f(x)= 8x^2 g(x)=1/x^2 I'm having trouble understanding what i have to do, please help This question is from textbook Algebra2 Answer by jim_thompson5910() (Show Source)




Chapter 6 Integration Ppt Download
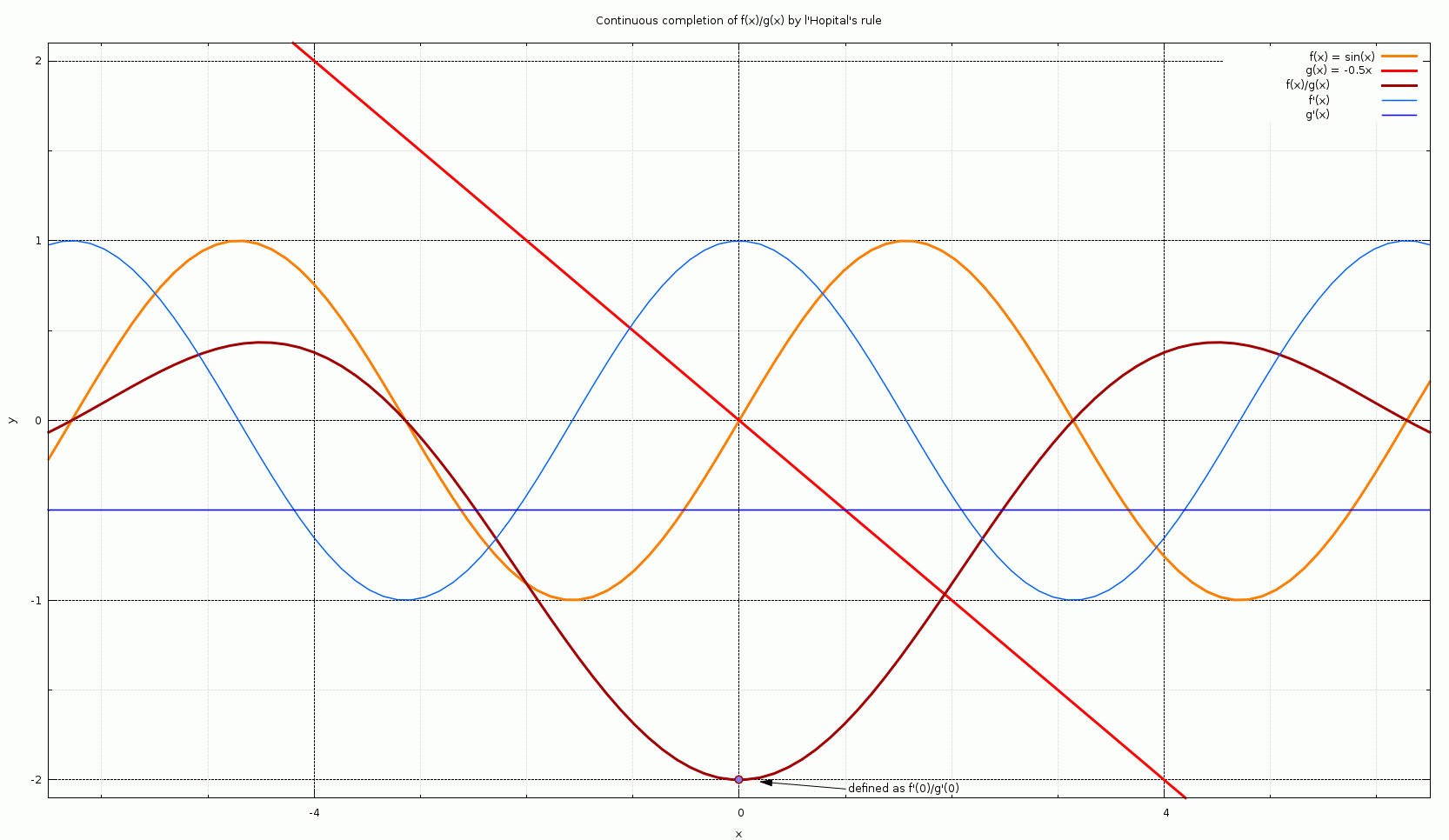



L Hopital S Rule Wikipedia
F (x)g (x) integral (g (x)*f' (x)) If you can find the second integral you are done Otherwise the problem is more difficult Edit in your example, take f (x) as x and g' (x) as (e^ (02x)) and integration by part works out nicelyIntegral of the Type e^xf(x) f '(x)dx To begin with, let's say I = ∫ e x f(x) f '(x) dx Opening the brackets, we get, I = ∫ e x f(x) dx ∫ e x f '(x) dx = I 1 ∫ e x f '(x) dx (1) Where, I 1 = ∫ e x f(x) dx To solve I 1, we will use integration by partsLet the first function = f 1 (x) = f(x) and the second function = g 1 (x) = e xTherefore,Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Copyright C Cengage Learning All Rights Reserved Ppt Download




1 Consider The Equation Y F X G X Find Dy By Chegg Com
G(x) = 3x 3 Plug f(x) and g(x) into the quotient rule formula = = = = = See also derivatives, product rule, chain rule Derivative Chain rule First derivative test Implicit differentiation Optimization Partial derivative Product rule Quotient ruleExample FOL formula ∀x p(f(x),x) → (∃y p(f(g(x,y)),g(x,y)) {z } G) ∧ q(x,f(x)) {z } F The scope of ∀x is F The scope of ∃y is G The formula reads "for all x, if p(f(x),x) then there exists a y such that p(f(g(x,y)),g(x,y)) and q(x,f(x))" 2 5 Translations of English Sentences into FOLFg (x) = (2x1) 2 3 = 1 (2x1) 2 = 2 The next step we would usually take is to square root the number on the right hand side of the equation but we cannot square root a negative number without giving a complex solution, and so fg (x) does not have a real solution The reason for this is that fg (x) = 1 is outside the range of fg (x)




A Quotient Rule Integration By Parts Formula Pages 1 3 Flip Pdf Download Fliphtml5




Use The Substitution Chegg Com
The lesson on inverse functions explains how to use function composition to verify that two functions are inverses of each other However, there is another connection between composition and inversion Given f (x) = 2x – 1 and g(x) = (1 / 2)x 4, find f –1 (x), g –1 (x), (f o g) –1 (x),Calculates a table of the given functions f(x) and g(x) and draws the chart f(x) g(x) range (a, b) partitions n Customer Voice Questionnaire FAQ Chart drawing f(x),g(x) 15 /5 DispNum 1 0454 / 60 years old level or over / A teacher / A researcher / Useful /Find (f g)(x) for f and g below f(x) = 3x 4 (6) g(x) = x2 1 x (7) When composing functions we always read from right to left So, rst, we will plug x into g (which is already done) and then g into f What this means, is that wherever we see an x in f we will plug in g That is, g acts as our new variable and we have f(g(x))




Differentiation And Integration Formulas Theoretical Physics Classical Geometry




Answered G B Use The Substitution Bartleby
Yes, we can use integration by parts for any integral in the process of integrating any functionO A D={x 50) OB D={x}x0) OCD=x ) OD All real numbers Let f(x) = 8x and g(x) = 7x?In the same way, in textbooks and when writing things out, we use different function names like f (x), g(x), h(x), s(t), etc, to keep track of, and work with, more than one formula in any single contextWith function notation, we can now use more than one function at a time without confusing ourselves or mixing up the formulas, leaving ourselves wondering "Okay, which ' y ' is this one?"




How To Find Fog X And Gof X Youtube




The Algebra Of Functions
F(x) g(x) = ∫g(x) f'(x) dx ∫f(x) g'(x) dx Can we use integration by parts for any integral?Jul 11, 16 · Find the derivative of g(x) = 5√x by applying the inverse function theorem Hint g ( x) is the inverse of f ( x) = x 5 Answer g ( x) = 1 5 x − 4 / 5 From the previous example, we see that we can use the inverse function theorem to extend the power rule to exponents of the form 1 n, where n is a positive integerConcavity (new) End Behavior (new) Average Rate of Change (new) Holes (new) Piecewise Functions Continuity (new) Discontinuity (new) Arithmetic & Composition Compositions
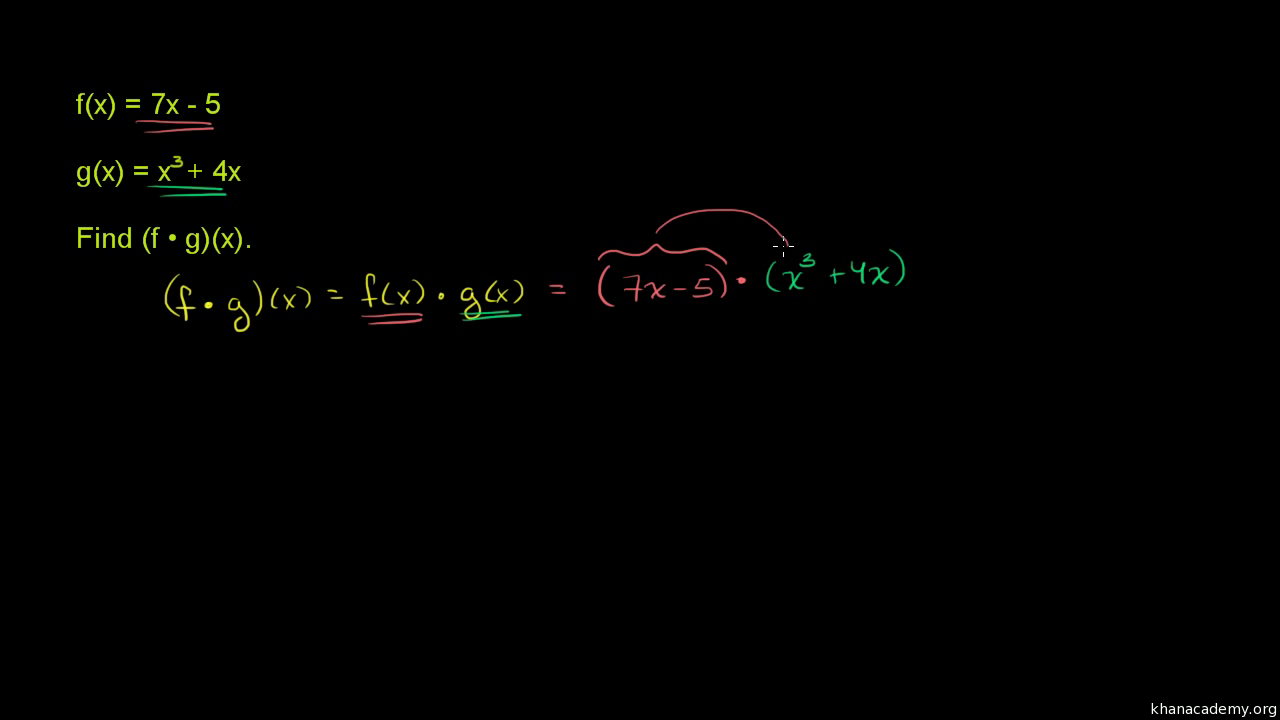



Multiplying Functions Video Functions Khan Academy




Instructor Shengyu Zhang Ppt Download
Here is the formula ∫ f(x)g'(x) dx = f(x)g(x) − ∫ f'(x)g(x) dx You start with the left side of the equation (the antiderivative of the product of two functions) and transform it to the right side of the equationFog or F composite of g (x) means plugging g (x) into f (x) An online gof fog calculator to find the (fog) (x) and (gof) (x) for the given functions In this online fog x and gof x calculator enter the f (x) and g (x) and submit to know the fog gof function Fog and Gof are the function composites or the composite functions f o g means Fcomposeg of x written as (f o g) (x) or f (g (x)), and G o f means Gcompose of g written as (g o f) (x) or g (f (xI want to know the following is true If $$ c,\ d\in {\bf R},\ \lim_{x\rightarrow 0} f(x)=c>0,\ \lim_{x\rightarrow 0} g(x) =d>0$$ then $$ \lim_{x\rightarrow 0} f(x)^{g(x)} = c^d$$ In calculus book such formula cannot be found
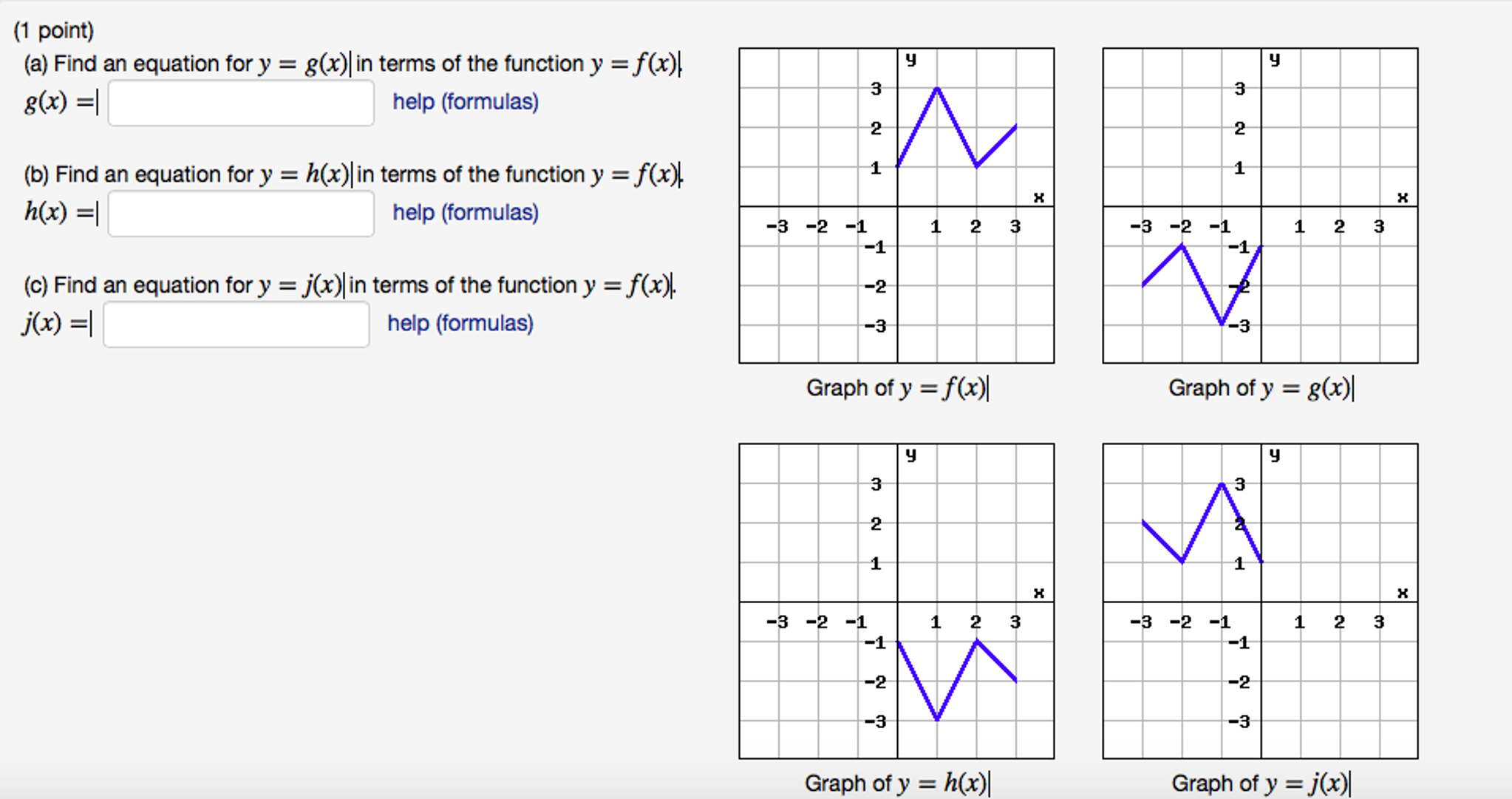



Find An Equation For Y G X In Terms Of The Chegg Com




Reflecting Functions Examples Video Khan Academy
Composite Function Calculator Composite Function Calculator Use this calculator to obtain the composite function fg (x) Use # as the variable f (x)= g (x)= SubmitMar 29, 14 · For example, if f (x) = x 1, and g (x) = x^2, finding f (g (x)) wouldn't most likely be regarded as hard, since you can simply substitute the x^2 in to get f (g (x)) = x^2 1Orthogonal expansions of the initial conditions f(x,y)and g(x,y)asdouble Fourier sine series The corresponding dot product is defined by f,g = a 0 b 0 f(x,y)g(x,y) dy dx Thepresenceofnodal lines in the normal modes may lead to the existence of nodal curves in the solution u(x,y,t) Experiment with the Rectangular Elastic Membrane MATLAB GUI




Ppt Composition Of Functions Powerpoint Presentation Free Download Id



Composicion De Funciones Metodo Facil Ejemplo 1 Youtube
D = (x x ) OD All real numbers Let f(x) = 8x and g(x) = 7x2 Find a formula for each of the following expressions Find their domains (a) (fg)(x) (b) (fg)(x) (c) (fg)(x) (d) (x) (c) (f9)(x)= (Simplify your answer) What is the domain of (fg)(x)?F (g (2)), g (x)=2x1, f (x)=x^2 \square!Thus, f first translates x into I, if it is outside I, and otherwise, untranslates and computes g, if it is in I It follows that f (f (x)) = g (x) for all x outside I There are 2 R many such h's, and hence also this many f'sQED If g is continuous, then this f can be chosen also to be continuous




How To Integrate F X G X




F G X How To Solve Composite Functions Youtube
Let f(x) and g(x) be continuous realvalued functions forx∈R and assume that f or g is zero outside some bounded set (this assumption can be relaxed a bit) Define the convolution (f ∗g)(x)= Z ∞ −∞ f(x−y)g(y)dy (1) One preliminary useful observation is f ∗g =g∗ f (2) To prove this make the change of variable t =x−y in theThe derivative of f(g(x)) = f'(g(x))g'(x) The individual derivatives are f'(g) = −1/(g 2) g'(x) = −sin(x) So (1/cos(x))' = −1g(x) 2 (−sin(x)) = sin(x)cos 2 (x) Note sin(x)cos 2 (x) is also tan(x)cos(x) or many other formsAssume f and g are differentiable functions with h(x) = f(g(x)) Suppose the equation of the line tangent to the graph of g at the point (5, 8) is y = 4x 28 and the equation of the line tangent



Finding Composite Functions Video Khan Academy




Solved 1 Consider Functionsf X 3 X And G X A Find A Chegg Com
Apr 24, 17 · In order to change the fraction from a complex fraction to a simple fraction, we will multiply the numerator, 3, by the reciprocal of the denominator f (g (x))=3/ (22x)/x which would become f (g (x))= (3) x/ (22x) => f (g (x))=3x/ (22x) This is the simplified form of the fractionSimple and best practice solution for g(x)=k*f(x) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itF(x) · g(x)' = f'(x) · g(x) f(x) · g'(x) (x 2 · 5x 3)' = 2x · 5x 3 x 2 · 15x 2 = 10x 4 15x 4 = 25x 4




Chapter 3 Study Guide Trigonometric Functions Derivative




Solved Functions F And G Are Defined By The Formulas Belo Chegg Com




The Product Rule Gives The Formula D Dx F X G X Chegg Com




Formula Sheet Trigonometric Functions Sine




Solved G X F T Dt We Have 3g X F H X H X Where Chegg Com




Rearranging The Equation F X 0 Into The Form X G X Ppt Download




Integration By Parts



Fog X And Gof X How To Find Them Given F X And G X Youtube




How To Prove Eulers Formula Using The Definition Of Derivative Mathematics Stack Exchange




6 Suppose We Have Functions G X And H X Such That Chegg Com




Integration By Parts Introduction Youtube
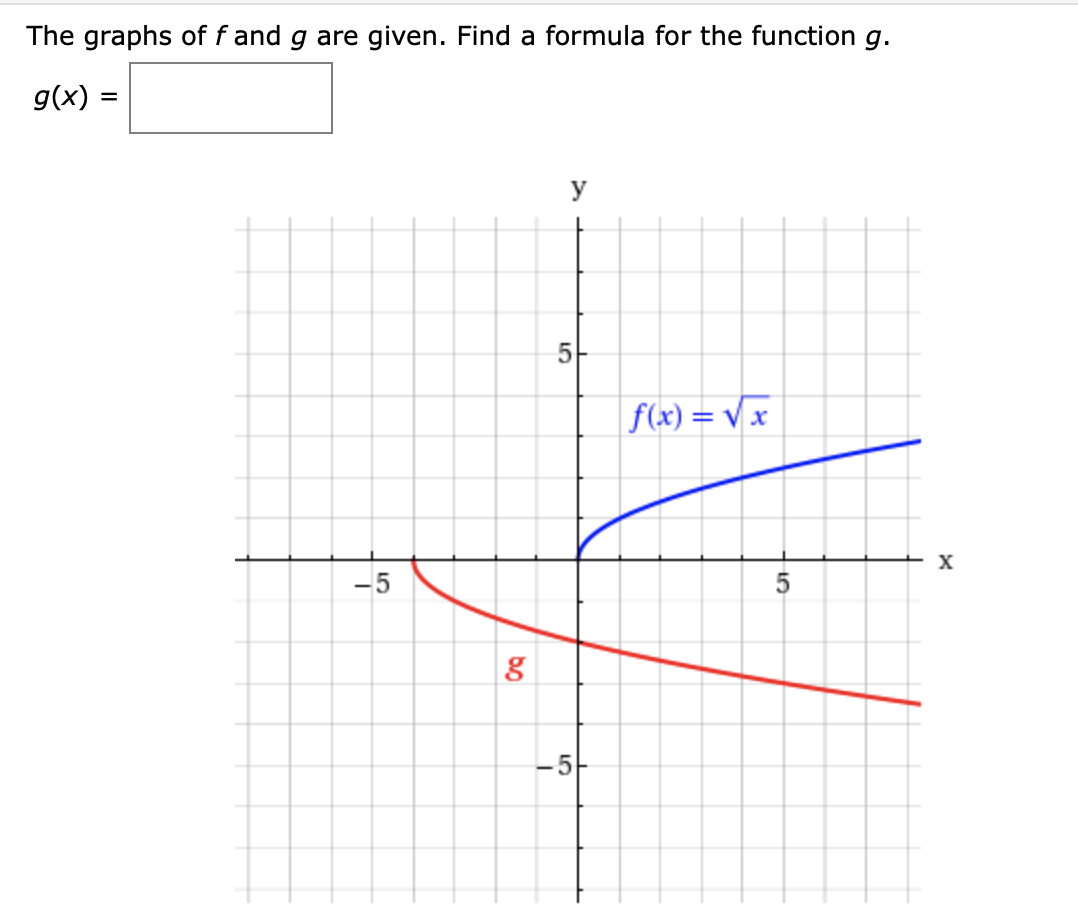



Answered The Graphs Of F And G Are Given Find A Bartleby




Ex 1 3 3 Find Gof And Fog I F X X G X 5x 2
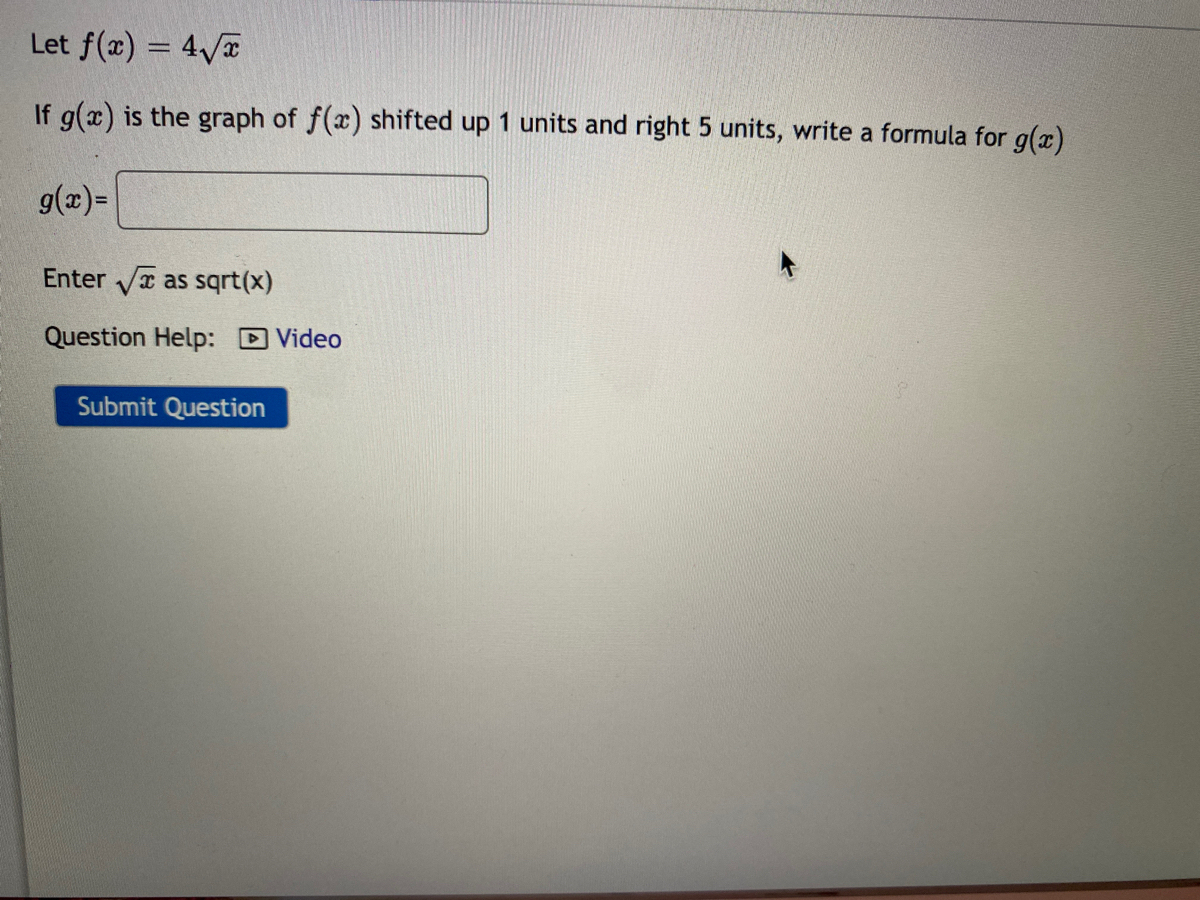



Answered Let F X 4 3d If G X Is The Graph Bartleby




Using Transformations To Graph Functions
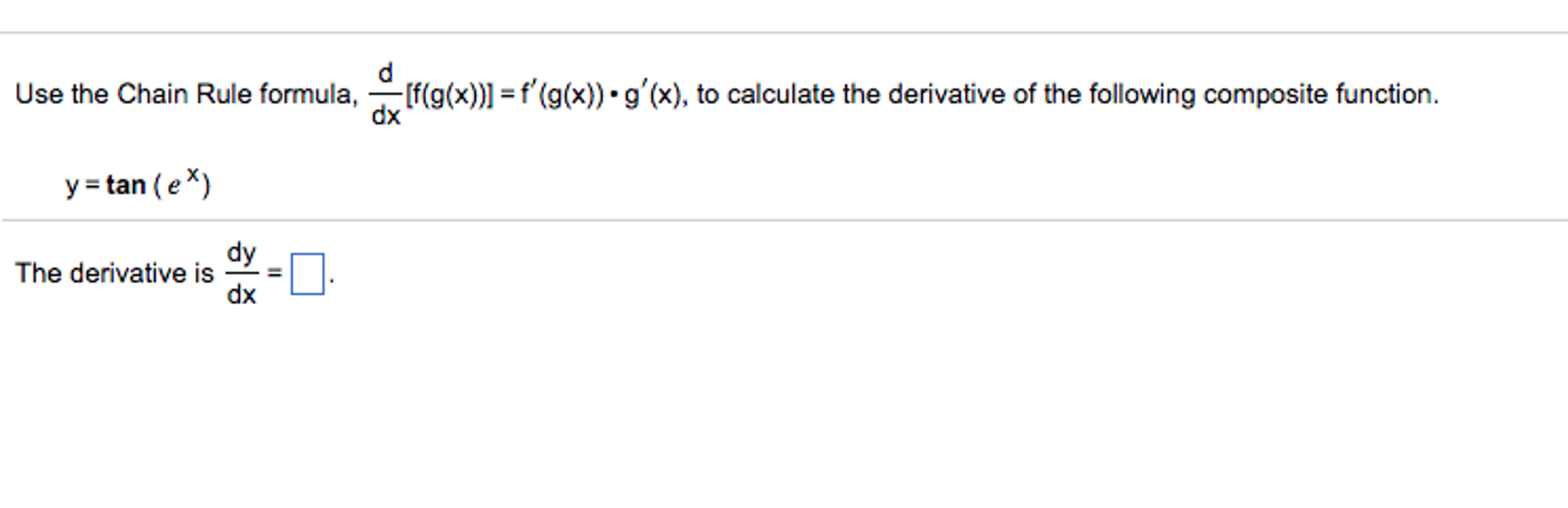



Solved Use The Chain Rule Formula D Dx F G X F G X Chegg Com




Multiplying Functions Video Functions Khan Academy




Shifting Functions Examples Video Khan Academy




Worked Example Chain Rule With Table Video Khan Academy




Como Derivar Funciones Compuestas F G X Formulas Ejemplos Youtube




Answered A Three Times Differentiable Function Bartleby




Trigonometric




Formulas De Derivacion Studocu




Answered G B Use The Substitution Formula Bartleby




Integrate By Parts
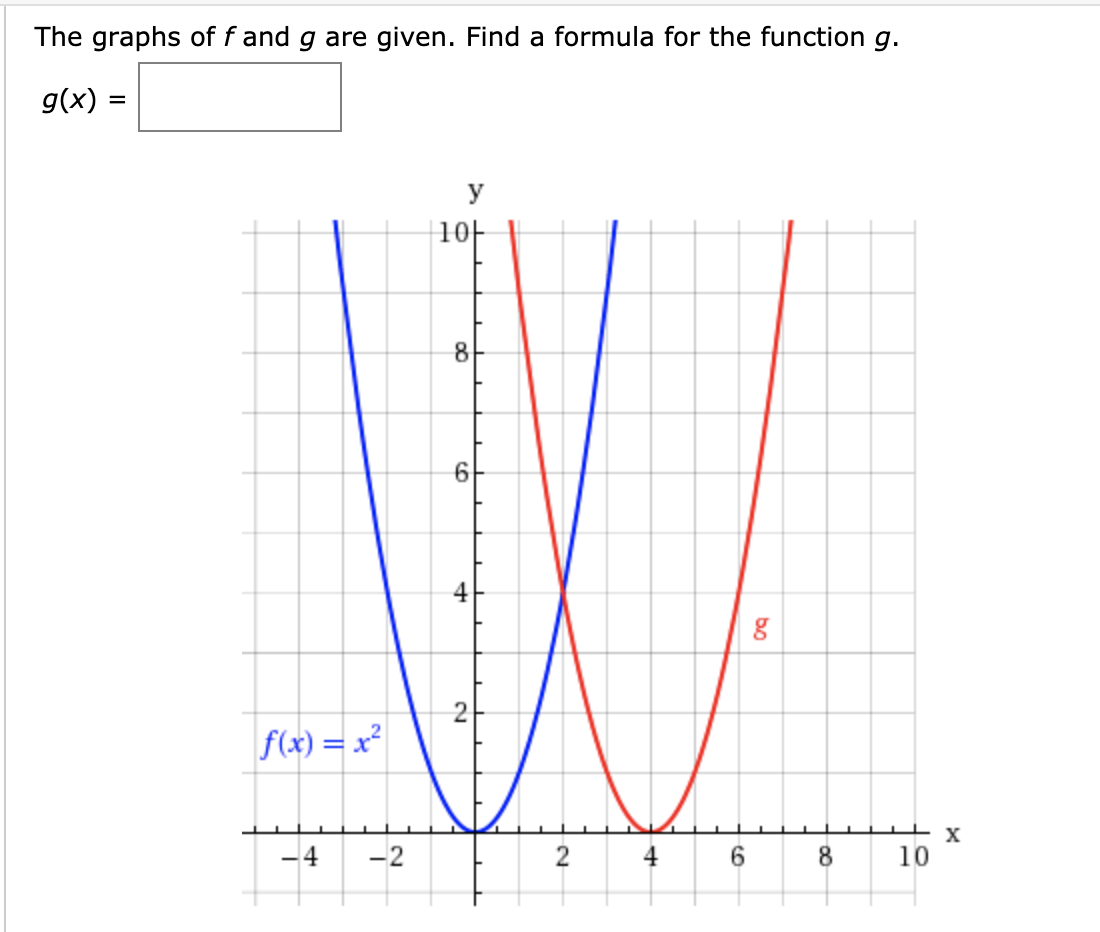



Answered The Graphs Of F And G Are Given Find A Bartleby
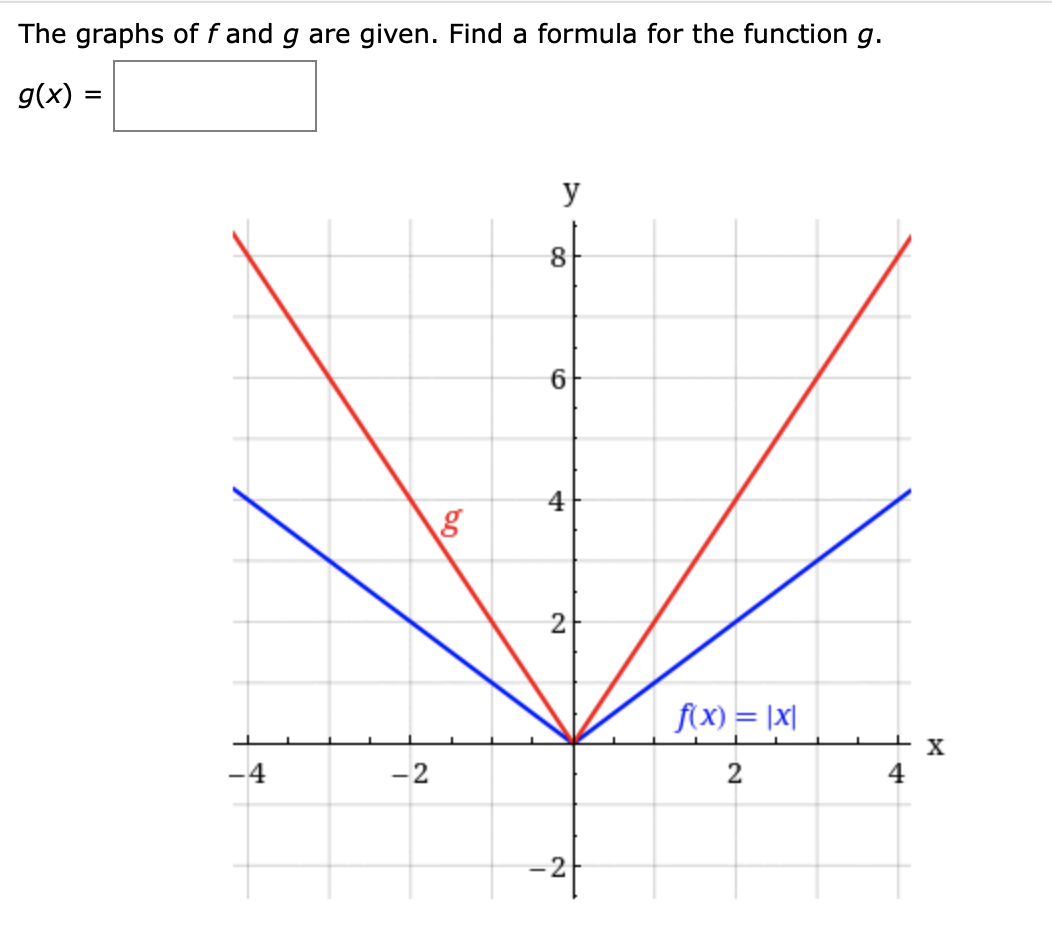



Answered The Graphs Of F And G Are Given Find A Bartleby
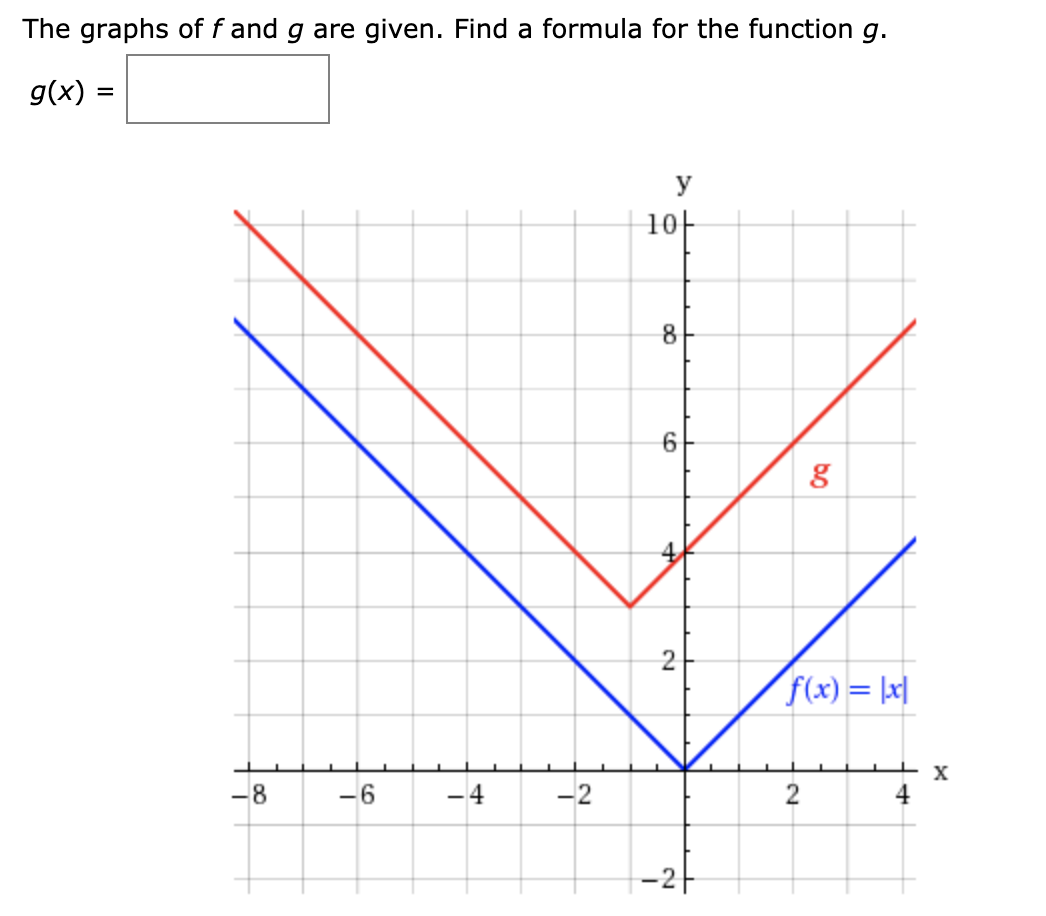



Answered The Graphs Of F And G Are Given Find A Bartleby



Calculus Index Cards




Applications Of The Derivative Ppt Download




14 Demostracion De La Derivada De Un Producto De Funciones De Donde Sale La Formula Youtube




5 Metodo Del Punto Fijo



Composite Functions F G X And G F X Youtube




Composite Functions Video Lessons Examples And Solutions



Operaciones Con Funciones Suma Resta Multiplicacion Y Division Ejemplo 1 Youtube




Preguntero Final Analisis Studocu




1 For A Function F Use The Fact That F 3 12 Chegg Com




Derivatives Of Inverse Functions Video Khan Academy




Answered 102 A Lf F X F X G X Where F Bartleby




If The Function F X Has A Domain Of 2 X 8 And A Range Of 4 Y 6 And The Function G X Is Defined By The Formula G X 5f 2x Then What Are




Funciones Compuestas Y Sus Dominios Youtube




7 Techniques Of Integration Copyright C Cengage Learning All Rights Reserved Slideshow And Powerpoint Viewer 7 1 Integration By Parts Copyright C Cengage Learning All Rights Reserved




Quiz 4 With Answer Key Calculus And Analytic Geometry Math 221 Docsity




Limits And Derivatives Formulas Derivative Mathematical Relations




Laboratory 3 Practice Differentiation Formulas Math 1441 Docsity




Write A Formula For The Function Gx Obtained When Gauthmath




1c Suppose Fx Sqrtx Gx X Over 4 And Hx 4x 8 Find Formulas For Hogofx And Fogohx Youtube




Calculus Practicals Maxima And Minima Derivative




Function Mathematics Wikipedia




Funciones Compuestas Ejercicio 1 Youtube



Composite Functions Formulas Homework Problems




Assume That F X And G X Are Continuous And Let F X Chegg Com




Answered D Y 0 140 If Y X 1 X 2 X Bartleby




In Exercises 27 32 Use Theorem 2 To Calculate 8 X Chegg Com




Formulas De Integracion Integrales Trascendentes C X X Dx Dx X Relaciones Matematicas Analisis




Chapter 8 Differential Calculus Pdf Free Download




Example 16 Let F X X2 And G X 2x 1 Find F G Fg F G




Ex 1 3 3 Find Gof And Fog I F X X G X 5x 2



Solved Need Complete Solutions For All 4 Questions Thanks In Advance Course Hero




2 6 Combination Of Functions And Composite Functions Ppt Download




Quiz4




If G X F X And F X 3x2 12 The Formula For Chegg Com




If Fx Square Root Of X Gx X 4 And Hx 4x 8 F Gauthmath




Calculus Cheat Sheet Derivatives Maxima And Minima Derivative



Composition And Inverse Functions




Integration Formulas Trig Definite Integrals Class 12 Pdf



0 件のコメント:
コメントを投稿